Derivadas

La derivada de la función f(x) en el punto x = a es el valor del límite, si existe, de un cociente incremental cuando el incremento de la variable tiende a cero.

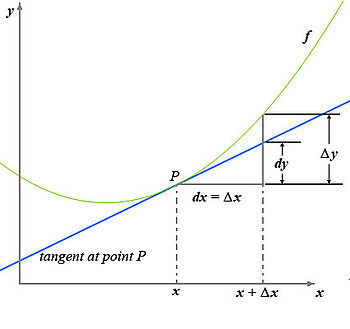
Derivada de una función

Considerando la función f definida en el intervalo abierto I y un punto a fijo en I, se tiene que la derivada de la función f en el punto  se define como sigue:

,

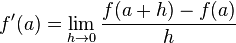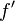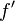si este límite existe, de lo contrario, , la derivada, no está definida. Esta última expresión coincide con la velocidad instantánea del movimiento continuo uniforme acelerado en cinemática.

A continuación relaciono tres documentos muy importantes que le será de mucha ayuda para una mayor comprensión de las derivadas. 

(Un libro taller para la enseñanza de la derivada en 11°)

https://drive.google.com/open?id=0BxqHa7pKYfpwVVlUWXBOR29Jb0U

(Taller N°1 de derivadas)

https://drive.google.com/open?id=0BxqHa7pKYfpwazhOUFVXQWlBUGc

(Taller N°2 de derivadas)

https://drive.google.com/open?id=0BxqHa7pKYfpwYjJ6S21BMmhCUVE