Circulo de las Matemáticas: Generalidades de la factorización

Factores
Se llaman factores o divisores a una expresión algebraica a las expresiones algebraicas que multiplicadas entre sí dan como producto la primera expresión.

FACTORIZACIÓN

Factorizar una expresión algebraica es hallar dos o más factores cuyo producto es igual a la expresión dada inicialmente.

La factorización puede considerarse como la operación inversa a la multiplicación, pues el propósito de ésta última es hallar el producto de dos o más factores; mientras que en la factorización, se buscan los factores de un producto dado.

Se llaman factores o divisores de una expresión algebraica, a los términos que multiplicados entre sí dan como producto la primera expresión.

Factorización

Multiplicación

Al factorizar una expresión, escribimos la expresión como un producto de sus factores. Supongamos que tenemos dos números 3 y 5 y se pide que los multipliquemos, escribiremos . En el proceso inverso, tenemos el producto 15 y se nos pide que lo factoricemos; entonces tendremos

Al factorizar el número 20, tendremos o .

En este ejemplo estamos factorizando y descomponiendo números como es el caso del 24 y 15, ahora miraremos un ejemplo donde utilizaremos variables o expresiones algebraicas:

Ejemplo:

De la expresión ab² + 3cb - b³ podemos factorizar b

y obtenemos la expresión: b(ab + 3c - b²)

Veamos paso a paso cómo se obtuvo la expresión:

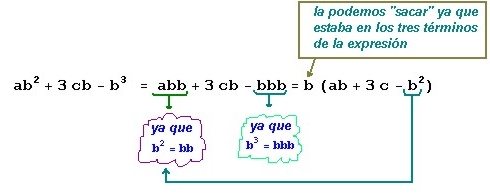
ahora podríamos reacomodar la expresión que queda dentro del paréntesis:

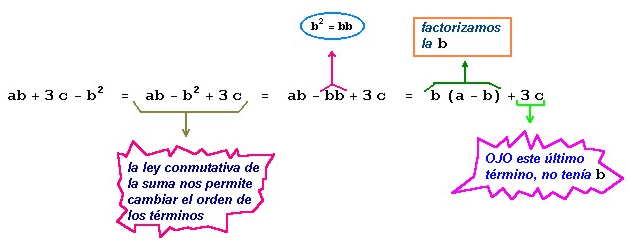
Finalmente si sustituimos este último resultado en la factorizacion inicial, obtenemos:

ab² + 3cb - b³ = b (b (a - b) + 3c)

ab² + 3cb - b³ = b (ab - b² + 3c)

ab² + 3cb - b³ = b (ab +3c –b²)

Con lo que vimos apenas estamos empezando a factorizar hay múltiples maneras de realizar esta tarea.

Si tenemos un binomio (dos expresiones) nos piden que la factoricemos y ellas están elevadas al cuadrado y entre ellas hay un signo negativo ¿ que hacemos ?

Hallamos las raíces de las expresiones y después la respuesta es igual a suma por diferencia. Por ejemplo:

a² − b² = (a + b) · (a − b)

Sacamos raices a a^{2 y}b^{2 y es igual a a y b}

Otro ejercicio mas claro

x⁴ − 16 = (x² + 4) · (x² − 4) =

= (x + 2) · (x − 2) · (x² + 4)

Las raíces son x = −2 y x = 2

Tenemos un trinomio pero en ella ni hay factor comun ni podemos rescribir ¿que hacemos?

Primero hay que tener en cuenta lo siguiente: Para descomponer en factores el trinomio de la forma P(x) = ax² + bx + c , se resuelve la ecuación de 2º grado. Si las soluciones a la ecuación son x₁ y x₂, el polinomio descompuesto será:

ax² + bx + c = a · (x − x₁) · (x − x₂)

Para ser un poco mas explícitos:

Si tenemos

, tenemos que tener en cuenta que el termino inicial sea cuadrado perfecto en este caso es la X hay que buscar dos numero multiplicados que me den 6 y que la suma y la resta de esos números me den 5 ¿cuales son? 3 y 2 ¿por qué? la multiplicación de ellos dos da 6 y la suma da 5. la respuesta es:

Ya con lo anterior podemos factorizar pero como todo hay un pero tenemos una suma y diferencia de cubos (las expresiones están elevadas a la tres) de dos expresiones algebraicas.

Es fácil verificar, mediante la multiplicación del segundo miembro de cada ecuación, las siguientes fórmulas de factorización para la suma y la diferencia de dos cubos.